 |
| Hassan Ammar/Associated Press |
In this World Cup, I was surprised when I saw a referee draw a white line on the ground for a free kick. "What a great idea!" I thought. But how does it work? Numerous google searches turned up meaningless articles such as this that basically describe the working principle of the spray as "you spray it on the ground and it leaves a line." NO SHIT SHERLOCK...
So how does it really work? Well, the can is under pressure, probably somewhere around 5 atmospheres of pressure, depending on the strength of the can. The main ingredient is water (80%). A mixture of gases are used to propel the surfactant out of the can, including butane, isobutane, and propane. Once the high pressure mixture of ingredients leave the can and enters the atmosphere, they expand and create a foam on the grass.
The most important ingredient is "polyoxyethylenated sorbitan monolaurate" (aka Tween20 at a concentration of around 1%). This molecule is known as a surfactant (more about this later!) The chemical structure is shown here (from Wikipedia):
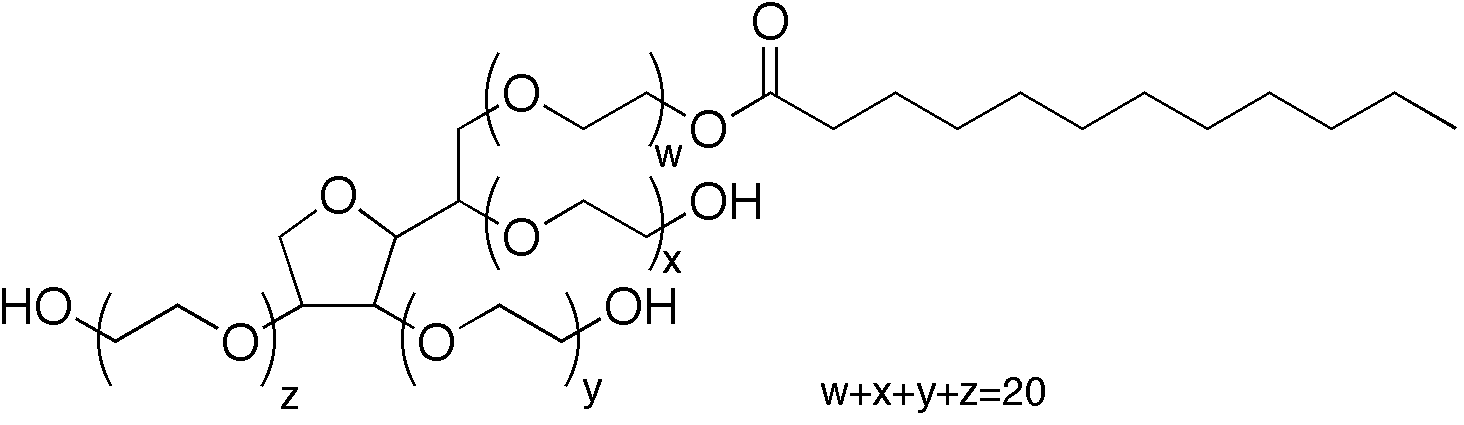
There are also some preservatives to prevent Bacteria from growing in the spray can if it's left on a shelf for a long time.
My interpretation of how the spray works is based mainly on the patent by the inventor that I found here: http://www.google.com/patents/US20120148741

Looking at this molecule, the left side is hydrophillic (likes water) and the right side is hydrophobic (likes sticking to hydrocarbon molecules such as butane, isobutane, and propane!) This is the key concept of how a surfactant works: it will stick to the interface between the water and the butane, to form surfaces. This allows the butane to form small drops in water (an emulsion) instead of just phase-separating with all the butane in one half of the can and the water in the other half of the can.
The other key concept is the phase change that Butane undergoes. The hydrocarbons that are under pressure (I would guess 5 atmospheres of pressure) in the can, expand to many times their volume when the enter the atmosphere. This is because Butane is a liquid at room temperature, for pressures greater than 2.5 atmospheres (density of 599 kg/m^3), but it is a gas at pressures below 2.5 atmospheres (density of 2.48 kg/m^3). So the Butane expands to ~250 times its volume when it leaves the can. It turns from a liquid into a gas and expands into massive bubbles. The water in the can doesn't change volume because it's a liquid at both atmospheric and can pressures.
So the expanded butane drops make a foam on the grass, which scatters light and makes it white in appearance. In my drawing, I only showed a few bubbles, but in reality there will be billions of them.
Eventually, the bubbles of propane will combine, pop, and evaporate, leaving only a residue of the surfactant (Tween20) and water on the grass. What makes the bubbles scatter light is the billions of interfaces of differing refractive indexes. Once these interfaces combine to form a thin layer of Tween20, they no longer scatter light, and become invisible.
Now you know: that's how World Cup Spray works!
Some of the other ingredients in the can are: a chelating agent "tetrasodium EDTA acid" at around 2% composition. A chelating agent is basically just a chemical that binds to metal ions. Who cares about metal ions? Well, metal ions (such as those that make up the can) have a tendency to break polymer chains such as the one that is used in the foam. So basically, the chelating agent helps preserve the important Tween20 chains from breaking down during storage in the can.
There are also some preservatives to prevent Bacteria from growing in the spray can if it's left on a shelf for a long time.
I made a schematic diagram of how I understand the can's operating principles. If you have questions, or think that my interpretation is wrong, please let me know and I'll update it! In particular, I'm not sure about the exact state of the foam while it's on the grass surface. Are they bubbles of propane? Or maybe not spherical bubbles?
My interpretation of how the spray works is based mainly on the patent by the inventor that I found here: http://www.google.com/patents/US20120148741







